HiGraf Graphics Routines
John Farrell and D. B. Holtkamp
All of these routines (except the contour plotting routines)
are copyrighted (1989) by John Farrell and David B.
Holtkamp, Los Alamos, New Mexico. The contour plotting
routines are copyrighted (1988) by Neil Judell, Optimal
Systems, Laboratory,Plainfield, NJ. These routines are
released to the Public Domain and may be freely distributed.
They may not be resold by anyone (besides us, of course!).
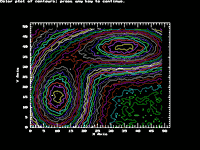 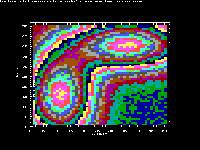 These routines are a set of high level graphics routines in
Turbo Pascal (version 5.x) that can be used for scientific
graphics. The header of the unit is appended to this
writeup. Four demo programs are included that demonstrates
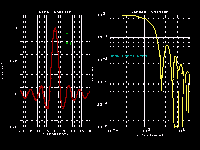
many of the routines. The first (GRAFTEST.PAS) demonstrates
the core routines of plotting data and curves with log or
linear axes. There is a contour plotting demo (CONTEST.PAS)
that synthesizes some data and plots it in contour plots of
three different types: contour lines in color, contour lines
in monochrome, and a "color contour" plot. The other two
routines demonstrate the cursor (CRSRTEST.PAS) and
crosshairs (CRHRTEST.PAS) packages in HiGraf.
First, a couple of words about graphics directories and
hardware. If the "TPDirectory" compiler directive is defined
at the top of HIGRAF.PAS, the BGI routines will
automatically detect the graphics hardware present in your
machine and load a graphics driver from a directory "C:\TP"
(this directory is defined in a procedure named
Initialize_Graph in HiGraf). If the "DefaultDirectory"
compiler directive is defined, then InitGraph will look for
the BGI drivers in the default directory.
If you wish to force the BGI routines to run in a particular
graphics mode (i.e. the IBM8514 or ATT400 mode on a Compaq)
or use the AutoMode detect function in InitGraph, choose the
desired compiler directive to suit your taste.
The program calling the HiGraf routines must use two data
types defined in HIGRAF:
TYPE
FLOAT = EXTENDED;
LINLOG = (lin,log);
These are used in the routines along with more familiar data
types.
The basic sequence for using the HiGraf routines is to :
Initialize_Graph; {sets up hardware}
Setup_Graph(....); {sets up software variables, etc}
Axes(...) or Frame(...); {displays axes}
Label_Axes(...); {labels axes}
TopTitle(...); {labels the top of the plot}
XAxisTitle(...) and YAxisTitle(...); {axes labels}
(do plotting commands: PlotData(...) or PlotPoint(...)
or
combinations of Move(...) and Draw(...) or somesuch)
Then Pause somehow...
CloseGraph; {BGI closout of graphics}
That's all there is to it. Take a look at the demo program
(GRAFTEST.PAS) for more complete details and examples. This
short example program displays two plots with linear and log
axes, data points, and other features.
These routines are a set of high level graphics routines in
Turbo Pascal (version 5.x) that can be used for scientific
graphics. The header of the unit is appended to this
writeup. Four demo programs are included that demonstrates
many of the routines. The first (GRAFTEST.PAS) demonstrates
the core routines of plotting data and curves with log or
linear axes. There is a contour plotting demo (CONTEST.PAS)
that synthesizes some data and plots it in contour plots of
three different types: contour lines in color, contour lines
in monochrome, and a "color contour" plot. The other two
routines demonstrate the cursor (CRSRTEST.PAS) and
crosshairs (CRHRTEST.PAS) packages in HiGraf.
First, a couple of words about graphics directories and
hardware. If the "TPDirectory" compiler directive is defined
at the top of HIGRAF.PAS, the BGI routines will
automatically detect the graphics hardware present in your
machine and load a graphics driver from a directory "C:\TP"
(this directory is defined in a procedure named
Initialize_Graph in HiGraf). If the "DefaultDirectory"
compiler directive is defined, then InitGraph will look for
the BGI drivers in the default directory.
If you wish to force the BGI routines to run in a particular
graphics mode (i.e. the IBM8514 or ATT400 mode on a Compaq)
or use the AutoMode detect function in InitGraph, choose the
desired compiler directive to suit your taste.
The program calling the HiGraf routines must use two data
types defined in HIGRAF:
TYPE
FLOAT = EXTENDED;
LINLOG = (lin,log);
These are used in the routines along with more familiar data
types.
The basic sequence for using the HiGraf routines is to :
Initialize_Graph; {sets up hardware}
Setup_Graph(....); {sets up software variables, etc}
Axes(...) or Frame(...); {displays axes}
Label_Axes(...); {labels axes}
TopTitle(...); {labels the top of the plot}
XAxisTitle(...) and YAxisTitle(...); {axes labels}
(do plotting commands: PlotData(...) or PlotPoint(...)
or
combinations of Move(...) and Draw(...) or somesuch)
Then Pause somehow...
CloseGraph; {BGI closout of graphics}
That's all there is to it. Take a look at the demo program
(GRAFTEST.PAS) for more complete details and examples. This
short example program displays two plots with linear and log
axes, data points, and other features.
 The following is a listing of the routines in the HIGRAF.PAS
unit. A couple of definitions are in order first:
World Coordinates: this coordinate system is the one usually
used for the plot data; these are FLOAT variables describing
the data values: i.e. x=1.27,y=1.366E-4, etc.
Screen Coordinates: these are the INTEGER numbers describing
the pixel addresses of each pixel; the upper left corner of
the physical screen is (0,0) in screen coordinates.
Additional Routines in SCALING.PAS
Another useful procedure is in SCALING.PAS; often in
producing plots, you have an array of data (with or without
error bars) that must be autoscaled. Scale_Axis (in
SCALING.PAS) takes pointers to these arrays, the type of
array it is (Byte, Word, etc), the number of values, and the
type of plot the axis is (Log or Linear). It returns "nice"
values for the minimum and maximum limits on the axis to be
plotted and a nice value for the axis labeling interval. One
way to use it is:
Scale_Axis(XData,NIL,Byte_Array,100,XWorldMin,XWorldMax,
XLabelArg,Lin);
Scale_Axis(YData,NIL,Byte_Array,100,
YWorldMin,YWorldMax,YLabelArg,Lin
Setup_Graph(XWorldMin,XWorldMax,YWorldMin,YWorldMax,
15,90,15,85,Lin,Lin);
Axes(0,0,XLabelArg/5,YLabelArg/5,5,5,FALSE);
Frame(XLabelArg/5,YLabelArg/5,5,5,FALSE);
Label_Axes(XLabelArg,YLabelArg);
This would give you "nice" axes with 5 minor tick marks
between axis labels in both X and Y.
Rapid Contour Plots By Bilinear Patch
by Neil Judell, Optimal Systems Laboratory,
Plainfield, NJ
In this technique, the points of the original data array are
viewed as being samples of a function that is continuous,
with piecewise continuous partial derivatives. This function
is presumed to be bilinear within the squares delineated by
the data points. In order to prepare the contour plot of the
entire region, we merely prepare a contour plot of each
square "patch" delineated by four adjacent data points.
There is one potential problem with this method, and that is
if a contour value is exactly equal to one of the data
values (one of the values exactly on the corner of a patch),
then the plot becomes ill-conditioned. In the software
example provided, this is readily prevented. The data values
take on only integer values, while the contour levels are
floating point. We simply prevent any contour value from
taking on an exact integer value by adding a small number
(constant called epsilon) if we determine that the contour
value is an exact integer.
Once this conditioning problem is resolved, it may readily
be seen that within a single patch, for a specified contour
level, exactly three possibilities exist: no contour line
crosses the patch, determined if the contour level is either
less than the minimum of the four corner values or greater
than the maximum of the corner values; one contour line
crosses the patch; or two contour lines cross the patch. In
the case where one contour line crosses the patch, the
bilinear equation is solved for the endpoints of the contour
line and the line is plotted. In the case where two contour
lines cross the patch, we determine the four endpoints, and
then must decide which pairs of endpoints to match to draw
the appropriate contour lines. Define the bilinear
coefficients for the patch in a coordinate system local to
the patch, so that the x value ranges from 0 to 1 and the y
value ranges from 0 to 1, and let the bilinear equation be:
value(x,y) = ax + by + cxy +d.
If we now attempt to parametrize the contour line in x in
terms of y we find:
x = (value - contour level - by - d)/(a + cy).
We then see, that because of the nature of the local
coordinate system, one of the contour lines must have the y
value of both of its endpoints greater than -a/c, and the
other contour line must have both of its endpoints less than
-a/c. (It should be noted that because of the non-integral
nature of the contour level, we cannot have two contour
lines in a patch when c=0). This means that if we simply
sort the four endpoints in increasing value of their y-
values, that the two endpoints with the lowest y-values form
a pair for one contour line and the two endpoints with the
highest y-values form a pair for the other contour line.
In the software example provided, contour lines are
approximated by drawing straight lines from one edge of the
bilinear patch to the other. In cases where the number of
data points are large relative to the screen pixel density
(say 20 x 20 data points for an EGA display), this is
adequate for reasonable contour plots. If the data are
sparse, it may be desirable to plot the contour line more
accurately within the patch, using the parametrized equation
above.
The software example provided contains the definitions used
for the contour plotting software, and the pointers to the
data array and the contour level array. The procedure for
allocating memory to
these arrays must be user provided. The data array pointer
is called data_array_pointer, which points to longint data
points, via:
data=data_array_pointer^[x]^[y],
with 1<=x<max_x_size and 1<=y<max_y_size. The contour level
array points to type float , and is accessed via: contour
level = contours[i], with 1<=i<max_contours.
The only procedure available for external calling is
Contour_Plot, which performs the entire plot function.
The test program, CONTEST.PAS, is a skeleton of a general
user program employing the contour plot modules. It performs
the operations minimally necessary for operation. First, it
allocates storage. Then, it fills the data array. In this
example, the data array consists of a sum of two two-
dimensional Gaussians plus noise. The contour level array is
then filled with values (which should be in ascending
order). Initialize_Graph is called to set the display to
graphics mode, Contour_Plot is called to perform the plot,
and finally CloseGraph is called to return the display to
text mode.
The following is a listing of the routines in the HIGRAF.PAS
unit. A couple of definitions are in order first:
World Coordinates: this coordinate system is the one usually
used for the plot data; these are FLOAT variables describing
the data values: i.e. x=1.27,y=1.366E-4, etc.
Screen Coordinates: these are the INTEGER numbers describing
the pixel addresses of each pixel; the upper left corner of
the physical screen is (0,0) in screen coordinates.
Additional Routines in SCALING.PAS
Another useful procedure is in SCALING.PAS; often in
producing plots, you have an array of data (with or without
error bars) that must be autoscaled. Scale_Axis (in
SCALING.PAS) takes pointers to these arrays, the type of
array it is (Byte, Word, etc), the number of values, and the
type of plot the axis is (Log or Linear). It returns "nice"
values for the minimum and maximum limits on the axis to be
plotted and a nice value for the axis labeling interval. One
way to use it is:
Scale_Axis(XData,NIL,Byte_Array,100,XWorldMin,XWorldMax,
XLabelArg,Lin);
Scale_Axis(YData,NIL,Byte_Array,100,
YWorldMin,YWorldMax,YLabelArg,Lin
Setup_Graph(XWorldMin,XWorldMax,YWorldMin,YWorldMax,
15,90,15,85,Lin,Lin);
Axes(0,0,XLabelArg/5,YLabelArg/5,5,5,FALSE);
Frame(XLabelArg/5,YLabelArg/5,5,5,FALSE);
Label_Axes(XLabelArg,YLabelArg);
This would give you "nice" axes with 5 minor tick marks
between axis labels in both X and Y.
Rapid Contour Plots By Bilinear Patch
by Neil Judell, Optimal Systems Laboratory,
Plainfield, NJ
In this technique, the points of the original data array are
viewed as being samples of a function that is continuous,
with piecewise continuous partial derivatives. This function
is presumed to be bilinear within the squares delineated by
the data points. In order to prepare the contour plot of the
entire region, we merely prepare a contour plot of each
square "patch" delineated by four adjacent data points.
There is one potential problem with this method, and that is
if a contour value is exactly equal to one of the data
values (one of the values exactly on the corner of a patch),
then the plot becomes ill-conditioned. In the software
example provided, this is readily prevented. The data values
take on only integer values, while the contour levels are
floating point. We simply prevent any contour value from
taking on an exact integer value by adding a small number
(constant called epsilon) if we determine that the contour
value is an exact integer.
Once this conditioning problem is resolved, it may readily
be seen that within a single patch, for a specified contour
level, exactly three possibilities exist: no contour line
crosses the patch, determined if the contour level is either
less than the minimum of the four corner values or greater
than the maximum of the corner values; one contour line
crosses the patch; or two contour lines cross the patch. In
the case where one contour line crosses the patch, the
bilinear equation is solved for the endpoints of the contour
line and the line is plotted. In the case where two contour
lines cross the patch, we determine the four endpoints, and
then must decide which pairs of endpoints to match to draw
the appropriate contour lines. Define the bilinear
coefficients for the patch in a coordinate system local to
the patch, so that the x value ranges from 0 to 1 and the y
value ranges from 0 to 1, and let the bilinear equation be:
value(x,y) = ax + by + cxy +d.
If we now attempt to parametrize the contour line in x in
terms of y we find:
x = (value - contour level - by - d)/(a + cy).
We then see, that because of the nature of the local
coordinate system, one of the contour lines must have the y
value of both of its endpoints greater than -a/c, and the
other contour line must have both of its endpoints less than
-a/c. (It should be noted that because of the non-integral
nature of the contour level, we cannot have two contour
lines in a patch when c=0). This means that if we simply
sort the four endpoints in increasing value of their y-
values, that the two endpoints with the lowest y-values form
a pair for one contour line and the two endpoints with the
highest y-values form a pair for the other contour line.
In the software example provided, contour lines are
approximated by drawing straight lines from one edge of the
bilinear patch to the other. In cases where the number of
data points are large relative to the screen pixel density
(say 20 x 20 data points for an EGA display), this is
adequate for reasonable contour plots. If the data are
sparse, it may be desirable to plot the contour line more
accurately within the patch, using the parametrized equation
above.
The software example provided contains the definitions used
for the contour plotting software, and the pointers to the
data array and the contour level array. The procedure for
allocating memory to
these arrays must be user provided. The data array pointer
is called data_array_pointer, which points to longint data
points, via:
data=data_array_pointer^[x]^[y],
with 1<=x<max_x_size and 1<=y<max_y_size. The contour level
array points to type float , and is accessed via: contour
level = contours[i], with 1<=i<max_contours.
The only procedure available for external calling is
Contour_Plot, which performs the entire plot function.
The test program, CONTEST.PAS, is a skeleton of a general
user program employing the contour plot modules. It performs
the operations minimally necessary for operation. First, it
allocates storage. Then, it fills the data array. In this
example, the data array consists of a sum of two two-
dimensional Gaussians plus noise. The contour level array is
then filled with values (which should be in ascending
order). Initialize_Graph is called to set the display to
graphics mode, Contour_Plot is called to perform the plot,
and finally CloseGraph is called to return the display to
text mode.
|

