Домашний Компьютер

---

Прогулки со шляпой

Евгений Скляревский
30.01.2001

Прежде чем пояснить, при чём тут шляпа, определимся - кому это интересно. А интересно это многим счастливчикам, познавшим кайф нажимания клавиш на ПК, полётов на Turbo Pascal’е в мир узоров, поверхностей и всякой волшебной математической чепухи. Тут уж точно мир раскололся на две половины и вторая, большая, глядя на экран, спрашивает: “Ну и что? Какая от этого польза?”

- “Ну и ничего, пользы действительно никакой ...” Но и прекратить невозможно, всё время толкает: “А что если удвоить, зациклить, округлить, отразить ...”.

Так вот, всё вышесказанное имеет весьма приблизительное отношение к основной теме (и к другим тоже ) Давным-давно попалась мне на глаза красивая функция:

		       Sin(X2+Y2)
		Z = ----------------
		         X2+Y2

Полюбуемся ею вместе:

• трёхмерная поверхность
• синус должен дать “волны”
• должна быть некоторая “горбушка”
• убывает при удалении от начала координат каким-то образом
• симметрия относительно осей

Так и просится пощупать её на экране. А вот и вариант исполнения задумки:

PROGRAM SHLAPA;
USES GRAPH,DOS,CRT;
VAR
  GraphDriver, GraphMode, ErrorCode,X,X1,Y,Y1 : INTEGER;
  Q,W: REAL;
  U,Z:REAL;
  C: CHAR;
BEGIN
  GraphDriver:= Detect;
  InitGraph(GraphDriver,GraphMode,'');
  X1:=0 ; Y1:=0 ; Q:=-15;
  REPEAT
    W:=-10;
    REPEAT
      U:=0.29*Q*Q+0.29*W*W; {1}
      Z:=(5*SIN(U))/ U+5.3; {2}
      X:=TRUNC(300+27*(Q-W*COS(PI/4))); {3}
      Y:=TRUNC(350+27*(W*SIN(PI/4)-Z)); {4}
      IF W > -10 THEN LINE(X,Y,X1,Y1); {5}
      X1:=X ; Y1:=Y;
      W:=W+0.05 ;
      SETCOLOR(TRUNC(Z*7+7)); {6}
    UNTIL W>13 ;
    Q:=Q+0.05 ;
  UNTIL Q>18;
  C:=READKEY;
END.

Так вот: это и есть та самая шляпа с полями, вынесенная в заголовок.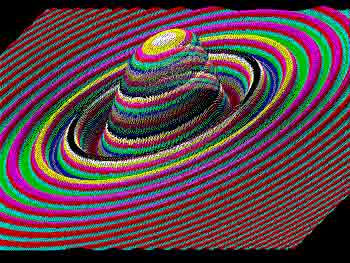

Причём на экран она выходит в аксонометрии, а угол наклона локальных осей шляпы относительно экранных можно попробовать поменять в строках {3} и {4} . Самые отчаянные могут попробовать разные значения углов для проекций на X и на Y, но от такой наглости трудно ожидать прогнозируемый результат. Гораздо интереснее поиграть коэффициентами:

     A * Sin( U )
Z = --------------      где U = C * X2 + D * Y2 + E * X * Y
        U + B

A - делает шляпу острее или положе

B - ещё и сдвигает её вдоль оси Z

C и D - сжимают шляпу вдоль осей X, Y

E - сжимает шляпу вдоль оси, проходящей под углом 45 градусов к осям XY

Для тех у кого две макушки, интересна замена: U = ( X - F ) * (X + F ) + Y2 . В результате шляпа раздваивается, разъезжается по оси X на величину 2*F. Аналогично можно раздвинуть шляпу и по Y:

U = ( X - F ) * ( X + F ) + ( Y - G ) * ( Y + G ), получив четырёх холмистую шляпу для рогатых мутантов.

Можно ещё поменять знак: U = X2 - Y2, превратив шляпу в нечто гиперболическое, на шляпу не похожее, в обиходе не встречающееся.

Шляпа рисуется ломаными линиями, с параметрами Q и W (локальными осями X и Y шляпы). Плавность линий зависит от величины приращений W, а частота линий от величины приращений Q. Чем меньше эти величины приращений, тем ярче шляпа, но дольше рисуется. Так что на Pentium’e можно получить шляпу поярче, а на 286-м - пореже.

А вы оценили раскраску шляпы? Цвет зависит от величины Z, меняя параметры можно получать пояски на тулье и на полях и даже волнистую шахматную доску.

Для самых занудных и въедливых читателей, ещё продолжающих читать этот бред, предлагаю попробовать поменять Sin(U) на Sin²(U), на Cos(U), на Sin(2*U) и вы будете вознаграждены открывшимися пейзажами - вокруг островка шляпы вдруг появляются лунные кратеры от гармоник высших порядков, объяснить которые с точки зрения тригонометрии и материализма невозможно.

А ещё можно попробовать поменять… но не буду лишать вас удовольствия самим поиграть и насладиться своим результатом. Шляпа хранит много приятных мгновений общения с ПК, достаньте их из неё.

P.S. И всё-таки невозможно удержаться: нарисуйте шляпу в полярных координатах - не пожалеете. А если центр этих координат не совпадает с центром шляпы . . .
Всё - ухожу, ухожу.

---

Домашний Компьютер