 | |||||||||||||||||||||||||||||||||
| Алгоритм преобразует алгоритм! | 
George Columbow
|
06.08.2001 | |||||||||||||||||||||||||||||||
| 
31k | ||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
Алгоритм преобразует алгоритм!Опубликовано в CitForum При программировании на Delphi или Паскале иногда попадаются задачи, которые трудно "втиснуть" в стандартные конструкции языка. А решение лежит совсем рядом - в теории конечных автоматов. Мы не будем залезать в дебри, а просто покажем как это делается.
Лирическое отступлениеОднажды, еще в школе, на уроке алгебры, я в первый раз услышал о существовании формальных преобразований. Помнится это были (a+b) 2. Это было нечто! Меня поразила сама возможность выполнять ряд простых шагов и гарантированно получать правильный результат. Ну а уж потом были примеры из тригонометрии: четырехэтажные дроби с ужасным количеством синусов, косинусов и бесконечно длинными аргументами, которые путем небольшой игры ума сворачивались в робкое 1+sin(x), а то и просто в неприметную 1. С тех самых пор я весьма неравнодушен к формальным преобразованиям и стараюсь найти им применение в программировании. И, вы знаете, иногда получается! :-)
Давным-давно, когда люди еще не придумали объектно-ориентированное программирование, модным направлением было программирование структурное. Шутки шутками, но в результате именно структурного подхода мы сейчас имеем Pascal и Delphi. Почему я говорю то Паскаль, то Дельфи? Просто потому, что лингвистическая основа Delphi - это Object Pascal, сильно выросший из детских штанишек, но все же узнаваемый. И новые объектно-ориентированные возможности и замечательные библиотеки классов в совокупности с CASE-средствами так и не скрыли полностью длинные уши структурного языка (и это замечательно!). Они вылезают то здесь, то там, в отдельных процедурах, в обработчиках событий... :-) Так вот, в те давние времена возникла следующая ситуация:
Но в начале - немного теории.
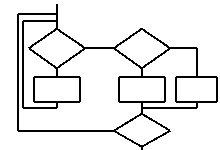
В нашем запутанном алгоритме наверняка не все так ужасно, как кажется. Скорее всего, там можно найти несколько фрагментов, подходящих под определение чисто структурных конструкций. Вопрос лишь в том, как эти конструкции соединить между собой. А вот в этом как раз может помочь наша рабочая лошадка - непотопляемая конструкция REPEAT-CASE. При умелом применении эта нехитрая пара команд может "переварить" алгоритм любой сложности и запутанности. Главное, чтобы ВЫ четко представляли что делаете. Однако хватит нам ходить вокруг да около, не пора ли заняться делом?
Осознание
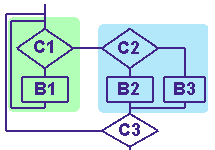
Проводя указанные действия несколько раз для разных алгоритмов, можно заметить, что на самом деле наши произвольно расставленные точки-состояния не такие уж случайные и произвольные. Как правило, при более глубоком рассмотрении вашего конкретного алгоритма можно найти каждому из этих состояний свое название. Это название может быть гораздо более выразительным, чем просто 1-2-3, поскольку это действительно состояния вашей программы. О чем я говорю? Пусть ваш алгоритм занимается, скажем, синтаксическим разбором HTML-файла. Тогда одно из состояний может звучать как "Обнаружен тэг BODY" или "Найден конец документа". Паскаль предлагает нам замечательное средство для работы с такими обозначениями в символическом виде и об этом средстве сейчас часто забывают. Программа из нашего примера может выглядеть так: var State:(START, EOF_found, Line_Added, DONE);
begin
State:=START; {для любого алгоритма}
repeat
case State of
START: begin B1; if C1 then State:=EOF_Found else State:=Line_Added end;
EOF_Found: begin B2; if C2 then State:=DONE else State:=Line_Added end;
Line_Added: begin B3; State:=START end;
end;
until State=DONE; {тоже для любого алгоритма}
end;
Замечательно, что Delphi все еще поддерживает эту спецификацию и
даже показывает при отладке символьное представление состояния! Это очень
удобно на практике. Спасибо, Borland!
Возможно вы, как и я, проделав подряд несколько таких преобразований и войдя во вкус, заметите, что стали мыслить при программировании чуть-чуть иначе. Иногда, особенно когда задача несколько запутана, хочется сразу выделить несколько важных состояний и строить обработчик уже вокруг них. Это правильное желание, ему стоит потакать. :-) Кстати, сейчас тема конечных автоматов вновь стала актуальной и то и дело мелькает на страницах компьютерных журналов.
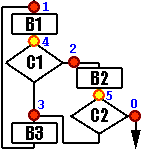
В нашем случае это означает добавление еще двух состояний - 4 и 5. Тогда программа примет вид: case State of
1: begin B1; State:=4 end;
2: begin B2; State:=5 end;
3: begin B3; State:=1 end;
4: if C1 then State:=2 else State:=3;
5: if C2 then State:=0 else State:=3;
end;
Хорошо это или плохо?
Хорошо, в том смысле, что даже при таком издевательстве программа не
перестает работать правильно. С другой стороны, посмотрите на исходный
код: где прозрачность, где легкость и ясность? Суть алгоритма растворена в
сплошных переходах состояний и из-за этого теряется.
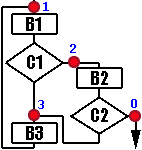 А что, если пойти в другую сторону и уменьшить число выделенных
состояний? В нашем примере реально только исключить состояние 2.
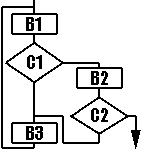
(Да, я знаю, на блок-схеме двойка есть, но давайте пока ее не замечать, OK? :) После "приведения подобных" программа будет иметь следующий вид: case State of
1: begin
B1; State:=3;
if C1 then begin
B2; if C2 then State:=0
end
end;
3: begin B3; State:=1 end;
end;
(Если непонятно, то здесь формально получаются две ветки
ELSE, ведущие обе к третьему состоянию. Если состояние вынести вверх, до
условия, то программа получается короче. Впрочем, это - дело вкуса :)
Как вам этот вариант? Мне кажется он тоже имеет право на жизнь, хотя лично мне вариант с четырьмя состояниями нравится больше. Как-то он нагляднее показывает что куда переходит и при каких условиях. А вам? Предвижу возражения такого толка, что при подобном подходе программы будут иметь повышенную склонность к зацикливанию. И да и нет. Циклы вообще склонны к зацикливанию :-) особенно если написать что-нибудь вроде repeat until false;. Так на то и голова дана, чтобы карась не дремал! А если серьезно, то устойчивость работы преобразованных таким образом программ прямо и недвусмысленно показывает, насколько удачно вы проработали исходную блок-схему и насколько аккуратно ее преобразовали. Поскольку на то оно и инвариантное преобразование, чтобы ничего не менять в смысле и логике программы, а затрагивать лишь ее внешнее представление.
И, наконец, мне нужно расставить точки над i. Я ни в коей мере не претендую на авторство в данном формальном подходе, более того, все проблемы и решения, изложенные в этой статье, известны уже довольно давно. Моя цель была просто напомнить вам об одном красивом, но, боюсь, забытом подходе к программированию на Паскале и Delphi. Пишите, если надумаете чем поделиться, |
|||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||
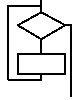
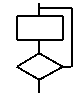
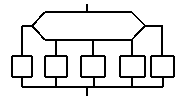
Как сказал один мудрый человек, "Идея, доведенная до
абсурда, часто превращается в свою противоположность". Давайте
попробуем довести наш метод до крайней степени.