| Этюды о бесполезной красоте - Рогатая гусеница |  Евгений Скляревский
Евгений Скляревский
|
25.09.2001 | ||
| 
40k | |||
|
Автор: Евгений
Скляревский
Адаптация для TMT Pascal: Валерий Вотинцев Оригинал статьи для Visual Basic: Журнал Hard'n'Soft Этюды
о бесполезной красоте
Этюд первый. Рогатая гусеница
Великий сказочник и математик сказал не всю правду. Гусеница была не столько синяя, сколько рогатая, причем рожек у нее было очень много, и в этом мы с вами скоро убедимся. Но прежде поговорим о торе. Напомню, тор - это тело, образованное вращением окружности вокруг оси, лежащей в плоскости этой окружности и не пересекающей ее. Самые очевидные примеры тора - бублики и камеры от велосипедного колеса. С тором, кстати, связано большое количество занимательных задач. Добавим только пару высоконаучных соображений. Если бы Земля была не шаром, а тором, то при ее столкновении с огромным астероидом он с высокой вероятностью пролетел бы в дырку. И еще: как было бы хорошо, если бы селекционеры вывели арбуз в форме тора - его было бы удобно переносить, продев руку в отверстие. Впрочем, нас сейчас тор интересует лишь как объект для рисования. Итак, компилируем приведенную ниже программу на TMT Pascal 3.50:
(***********************************************)
(* Рогатая гусеница *)
(* Автор алгоритма: Евгений Скляревский (VB) *)
(* ------------------------------------------- *)
(* Адаптация для TMT Pascal: *)
(* Валерий Вотинцев *)
(* MS-DOS 32-bit protected mode *)
(* Win32 Console application *)
(* Win32 GUI *)
(***********************************************)
uses CRT, Math, Graph;
var
i,j: integer;
t, s: extended;
ia,ja, RR, RR0, RR1: extended;
x, y, z: extended;
X1, Y1, X2, Y2, xx, yy: LongInt;
red, green, blue: byte;
begin
SetSVGAMode(800,600,16,LFBorBanked); // Установка графического режима
if GraphResult<>grOk then begin // Проверка результата
Writeln('Mode not supported..');
Halt(0);
end;
xx := 400; // Начало по Х
yy := 300; // Начало по Y
RR := 260; // Радиус в плоскости XZ
RR1 := 60; // Радиус "тела" тора
For i := 0 To 719 do begin
ia := i / 2.0; // Каждый шаг - пол-градуса
For j := 0 To 719 do begin
ja := j / 2; // Каждый шаг - пол-градуса
t := ia * Pi / 180; // Угловой параметр для большого круга
s := ja * Pi / 180; // Угловой параметр для малого круга
{1a} RR0 := RR1;
{1b} {RR0 := RR1 + 60 * IntPower(Sin(2 * t),2);}
{1c} {RR0 := RR1 + 60 * IntPower(Sin(2 * t),2) +
60 * IntPower(Sin(8 * s),24) * IntPower(Sin(16 * t),24);}
{1d} {RR0 := RR1 + 60 * IntPower(Sin(16 * s),24) * IntPower(Sin(32 * t),24);}
{1e} {RR0 := RR1 + 60 * IntPower(Sin(4 * s),24) * IntPower(Sin(8 * t),24);}
X := RR * Cos(t) + RR0 * Cos(s);
Y := RR0 * Sin(s);
{2a} z := RR * Sin(t) + RR0 * Cos(s);
{2b} {z := RR * Sin(2 * t) + RR0 * Cos(s);}
// Переводим координаты в плоскость экрана
X1 := trunc(X - z * Cos(Pi / 3) * 0.5);
Y1 := trunc(Y - z * Sin(Pi / 3) * 0.5);
red := trunc(RR0 * 255) div trunc(RR1 + 60); // Красный
green := trunc(255 * ia / 10) mod 255; // Зеленый
blue := trunc(0.1 * ia * ja) mod 255; // Синий
if (i = 0) and (j = 0) then begin
red := 0; // Чтобы начальную линию
green := 0; // не было видно,
blue := 0; // нарисуем ее черным цветом
end;
Line (X1 + xx, Y1 + yy, X2 + xx, Y2 + yy, RGBColor(red, green, blue));
X2 := X1;
Y2 := Y1;
end;
end;
ReadKey; // Ждем нажатия клавиши
CloseGraph;
end.
В программе мы запустили два цикла: с
переменной j (угловой параметр s для прорисовки малого круга с
радиусом RR1) и переменной i (угловой параметр t для вращения малого
круга в плоскости XZ радиусом RR). Проекцию оси Z направим под углом
60 градусов к оси X, а для перевода объемной картинки в плоскость
экрана используем переменные X1 и Y1.
Если в приведенном тексте
программы мы оставим все как есть, то на экране появится обычный тор.

Обратите внимание на его расцветку, она задается переменными red, green и blue. В приведенном примере красный цвет пропорционален текущему радиусу малого круга и проявляется только на <вздутиях> и рожках, зеленый пропорционален i, что дает поперечные полосы, а синий зависит от произведения i * j и проявляется в виде голубых полосок.
Насмотревшись на скромный и унылый тор, подумаем, как
бы его деформировать.
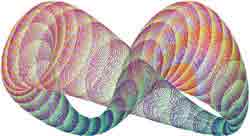
Теперь внесем <искажения> при вычислении RR0 за счет добавления еще одного слагаемого:
RR0 = RR1 + 60·Sin(2t)2
Мы получим картинку с "утолщениями", явно претендующую
на то, чтобы Зигмунд Фрейд предлагал ее своим пациентам для
диагностики психических отклонений.
Закомментируйте строку {1a} и уберите комментарий со строки {1b}.
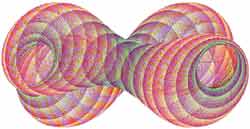
Опыты со слагаемым RR1 наиболее эффектны - попробуйте поменять множитель при синусе (60), множитель при t и показатель степени, в которую возводится синус (второй параметр функции IntPower). Вы будете вознаграждены появлением на экране загадочных существ. Однако подбираемся к главному - еще более усложним формулу вычисления для RR0, а именно добавим еще одно слагаемое с произведением синусов в разных степенях:
RR0 = RR1 + 60·Sin(2t)2 + 60·(Sin(8s))24·Sin(16t)24
Чтобы "запустить" эту формулу, раскомментируйте строку {1c}.
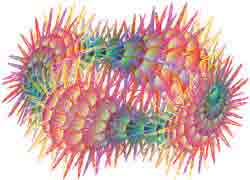
Первое слагаемое с RR1 дает
уже рассмотренные нами утолщения "туловища", а вот второе - рожки на торе, или,
точнее, уже на гусенице. Причем множитель при s дает количество
рожек на малом круге, множитель при t - на большом круге, показатели
степени определяют плавность или крутизну рожек, а передний числовой
множитель (60) - их высоту.

Теперь уменьшим количество рожек вдоль длины тела гусеницы
Если показатель степени при синусе нечетный, то отростки будут не только наружу, но и внутрь, придавая существам на экране довольно мерзопакостную внешность. По правде говоря, наша виртуальная гусеница получилась не столько с рожками, как было заявлено, сколько с колючками. 
|
||||